Как найти углы параллелограмма зная 1 угол. Параллелограмм

Образование

Средний уровень

Параллелограмм, прямоугольник, ромб, квадрат (2019)

1. Параллелограмм

Сложное слово «параллелограмм »? А скрывается за ним очень простая фигура.

Ну, то есть, взяли две параллельные прямые:

Пересекли ещё двумя:

И вот внутри - параллелограмм !

Какие же есть свойства у параллелограмма?

Свойства параллелограмма.

То есть, чем можно пользоваться, если в задаче дан параллелограмм ?

На этот вопрос отвечает следующая теорема:

Давай нарисуем все подробно.

Что означает первый пункт теоремы ? А то, что если у тебя ЕСТЬ параллелограмм, то непременно

Второй пункт означает, что если ЕСТЬ параллелограмм , то, опять же, непременно :

Ну, и наконец, третий пункт означает, что если у тебя ЕСТЬ параллелограмм, то обязательно:

Видишь, какое богатство выбора? Что же использовать в задаче? Попробуй ориентироваться на вопрос задачи, или просто пробуй все по очереди - какой-нибудь «ключик» да подойдёт.

А теперь зададимся другим вопросом: а как узнать параллелограмм «в лицо»? Что такое должно случиться с четырехугольником, чтобы мы имели право выдать ему «звание» параллелограмма?

На этот вопрос отвечает несколько признаков параллелограмма.

Признаки параллелограмма.

Внимание! Начинаем.

Паралелограмм.

Обрати внимание : если ты нашёл хотя бы один признак в своей задаче, то у тебя точно параллелограмм, и ты можешь пользоваться всеми свойствами параллелограмма.

2. Прямоугольник

Думаю, что для тебя вовсе не явится новостью то, что

Первый вопрос: а является ли прямоугольник параллелограммом?

Конечно, является! Ведь у него и - помнишь, наш признак 3 ?

А отсюда, конечно же, следует, что у прямоугольника, как и у всякого параллелограмма и, а диагонали точкой пересечения делятся пополам.

Но есть у прямоугольника и одно отличительное свойство.

Свойство прямоугольника

Почему это свойство отличительное? Потому что ни у какого другого параллелограмма не бывает равных диагоналей. Сформулируем более чётко.

Обрати внимание : чтобы стать прямоугольником, четырехугольнику нужно сперва стать параллелограммом, а потом уже предъявлять равенство диагоналей.

3. Ромб

И снова вопрос: ромб - это параллелограмм или нет?

С полным правом - параллелограмм , потому что у него и (вспоминаем наш признак 2 ).

И снова, раз ромб - параллелограмм , то он обязан обладать всеми свойствами параллелограмма. Это означает, что у ромба противоположные углы равны, противоположные стороны параллельны, а диагонали делятся точкой пересечения пополам.

Свойства ромба

Посмотри на картинку:

Как и в случае с прямоугольником, свойства эти - отличительные , то есть по каждому из этих свойств можно заключить, что перед нами не просто параллелограмм , а именно ромб.

Признаки ромба

И снова обрати внимание : должен быть не просто четырехугольник, у которого перпендикулярны диагонали, а именно параллелограмм . Убедись:

Нет, конечно, хотя его диагонали и перпендикулярны, а диагональ - биссектриса углов и. Но … диагонали не делятся, точкой пересечения пополам, поэтому - НЕ параллелограмм , а значит, и НЕ ромб .

То есть квадрат - это прямоугольник и ромб одновременно. Давай посмотрим, что из этого получится.

Понятно почему? - ромб - биссектриса угла A, который равен. Значит делит (да и тоже) на два угла по.

Ну, это совсем ясно: прямоугольник диагонали равны; ромб диагонали перпендикулярны, и вообще - параллелограмм диагонали делятся точкой пересечения пополам.

СРЕДНИЙ УРОВЕНЬ

Свойства четырехугольников. Параллелограмм

Свойства параллелограмма

Внимание! Слова «свойства параллелограмма » означают, что если у тебя в задаче есть параллелограмм, то всем нижеследующим можно пользоваться.

Теорема о свойствах параллелограмма.

В любом параллелограмме:

Давай-ка поймём, почему это всё верно, иными словами ДОКАЖЕМ теорему.

Итак, почему верно 1)?

Раз - параллелограмм, то:

как накрест лежащие
как накрест лежащие.

Значит, (по II признаку: и - общая.)

Ну вот, а раз, то и - всё! - доказали.

Но кстати! Мы ещё доказали при этом и 2)!

Почему? Но ведь (смотри на картинку), то есть, а именно потому, что.

Осталось только 3).

Для этого всё-таки придётся провести вторую диагональ.

И теперь видим, что - по II признаку (угла и сторона «между» ними).

Свойства доказали! Перейдём к признакам.

Признаки параллелограмма

Напомним, что признак параллелограмма отвечает на вопрос "как узнать?", что фигура является параллелограммом.

В значках это так:

Почему? Хорошо бы понять, почему - этого хватит. Но смотри:

Ну вот и разобрались, почему признак 1 верен.

Ну, это ещё легче! Снова проведём диагональ.

А значит:

И тоже несложно. Но …по-другому!

Значит, . Ух! Но и - внутренние односторонние при секущей!

Поэтому тот факт, что означает, что.

А если посмотришь с другой стороны, то и - внутренние односторонние при секущей! И поэтому.

Видишь, как здорово?!

И опять просто:

Точно так же, и.

Обрати внимание: если ты нашел хотя бы один признак параллелограмма в своей задаче, то у тебя точно параллелограмм, и ты можешь пользоваться всеми свойствами параллелограмма.

Для полной ясности посмотри на схему:

Свойства четырехугольников. Прямоугольник.

Свойства прямоугольника:

Пункт 1) совсем очевидный - ведь просто выполнен признак 3 ()

А пункт 2) - очень важный . Итак, докажем, что

А значит, по двум катетам (и - общий).

Ну вот, раз треугольники и равны, то у них и гипотенузы и тоже равны.

Доказали, что!

И представь себе, равенство диагоналей - отличительное свойство именно прямоугольника среди всех параллелограммов. То есть верно такое утверждение^

Давай поймём, почему?

Значит, (имеются в виду углы параллелограмма). Но ещё раз вспомним, что - параллелограмм, и поэтому.

Значит, . Ну и, конечно, из этого следует, что каждый из них по! Ведь в сумме-то они должны давать!

Вот и доказали, что если у параллелограмма вдруг (!) окажутся равные диагонали, то это точно прямоугольник .

Но! Обрати внимание! Речь идёт о параллелограммах ! Не любой четырехугольник с равными диагоналями - прямоугольник, а только параллелограмм!

Свойства четырехугольников. Ромб

И снова вопрос: ромб - это параллелограмм или нет?

С полным правом - параллелограмм, потому что у него и (Вспоминаем наш признак 2).

И снова, раз ромб - параллелограмм, то он обязан обладать всеми свойствами параллелограмма. Это означает, что у ромба противоположные углы равны, противоположные стороны параллельны, а диагонали делятся точкой пересечения пополам.

Но есть и особенные свойства. Формулируем.

Свойства ромба

Почему? Ну, раз ромб - это параллелограмм, то его диагонали делятся пополам.

Почему? Да, потому же!

Иными словами, диагонали и оказались биссектрисами углов ромба.

Как в случае с прямоугольником, свойства эти - отличительные , каждые из них является ещё и признаком ромба.

Признаки ромба.

А это почему? А посмотри,

Значит, и оба этих треугольника - равнобедренные.

Чтобы быть ромбом, четырёхугольник сперва должен «стать» параллелограммом, а потом уже демонстрировать признак 1 или признак 2.

Свойства четырехугольников. Квадрат

То есть квадрат - это прямоугольник и ромб одновременно. Давай посмотрим, что из этого получится.

Понятно, почему? Квадрат - ромб - биссектриса угла, который равен. Значит делит (да и тоже) на два угла по.

Почему? Ну, просто применим теорему Пифагора к.

КРАТКОЕ ИЗЛОЖЕНИЕ И ОСНОВНЫЕ ФОРМУЛЫ

Свойства параллелограмма:

Противоположные стороны равны: , .
Противоположные углы равны: , .
Углы при одной стороне составляют в сумме: , .
Диагонали делятся точкой пересечения пополам: .

Свойства прямоугольника:

Диагонали прямоугольника равны: .
Прямоугольник - параллелограмм (для прямоугольника выполняются все свойства параллелограмма).

Свойства ромба:

Диагонали ромба перпендикулярны: .
Диагонали ромба являются биссектрисами его углов: ; ; ; .
Ромб - параллелограмм (для ромба выполняются все свойства параллелограмма).

Свойства квадрата:

Квадрат - ромб и прямоугольник одновременно, следовательно для квадрата выполняются все свойства прямоугольника и ромба. А так же.

Параллелограммом называется такой четырехугольник, в котором противоположные стороны попарно параллельны.

Параллелограмм обладает всеми свойствами четырехугольников, но кроме этого имеет и свои отличительные особенности. Зная их, мы можем с легкостью находить как стороны, так и углы параллелограмма.

Свойства параллелограмма

Сумма углов в любом параллелограмме, как и в любом четырехугольнике, равна 360°.
Средние линии параллелограмма и его диагонали пересекаются в одной точке и делятся ею пополам. Эту точку принято называть центром симметрии параллелограмма.
Противоположные стороны у параллелограмма всегда равны.
Также у этой фигуры всегда равны противоположные углы.
Сумма углов, которые прилегают к любой из сторон параллелограмма, всегда составляет 180°.
Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон. Это выражается формулой:
- d 1 2 + d 2 2 = 2 (a 2 +b 2), где d 1 и d 2 - диагонали, a и b - смежные стороны.
Косинус тупого угла всегда меньше нуля.

Как найти углы заданного параллелограмма, применяя эти свойства на практике? И какие еще формулы могут нам в этом помочь? Рассмотрим конкретные задания, в которых требуют: найдите величины углов параллелограмма.

Нахождение углов параллелограмма

Случай 1. Известна мера тупого угла, требуется найти острый угол.

Пример: В параллелограмме ABCD угол A равен 120°. Найдите меру остальных углов.

Решение: Пользуясь свойством № 5, мы можем найти меру угла B, смежного с тем углом, который дан в задании. Он будет равен:

180°-120°= 60°

А теперь, пользуясь свойством №4, мы определяем, что два оставшихся угла C и D противоположны тем углам, которые мы уже нашли. Угол C противоположен углу A, угол D - углу B. А следовательно они попарно им равны.

Ответ: B = 60°, C = 120°, D=60°

Случай 2. Известны длины сторон и диагонали

В таком случае нам необходимо воспользоваться теоремой косинусов.

Мы можем сначала по формуле вычислить косинус нужного нам угла, а потом по специальной таблице найти, чему равен сам угол.

Для острого угла формула такая:

cosa = (А² + В² - d²) / (2 * А * В), где
а - это искомый острый угол,
А и В - стороны параллелограмма,
d - меньшая диагональ

Для тупого угла формула немного меняется:

cosß = (А² + В² - D²) / (2 * А * В), где
ß - это тупой угол,
А и В - стороны,
D - большая диагональ

Пример: необходимо найти острый угол параллелограмма, стороны которого равны 6 см и 3 см, а меньшая диагональ равна 5.2 см

Подставляем значения в формулу для нахождения острого угла:

cosa = (6 2 + 3 2 - 5.2 2) / (2 * 6 * 3) = (36 + 9 - 27.04) / (2 * 18) = 17.96/36 ~ 18/36 ~1/2
cosa = 1/2. По таблице выясняем, что искомый угол равен 60°.

Параллелограммом называется четырехугольник, у которго противоположные стороны параллельны, т.е. лежат на параллельных прямых

Свойства параллелограмма: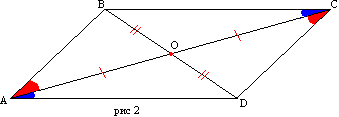
Теорема 22. Противоположные стороны параллелограма равны.
Доказательство. В параллелограмме АВСD проведем диагональ АС. Треугольники АСD и АСВ равны, как имеющие общую сторону АС и две пары равных углов. прилежащих к ней: ∠ САВ=∠ АСD, ∠ АСВ=∠ DAC (как накрест лежащие углы при параллельных прямых AD и ВС). Значит, АВ=CD и ВС=AD, как соответственные стороны равных треугольников, ч.т.д. Из равенства этих треугольников также следует равенство соответственных углов треугольников:
Теорема 23. Противоположные углы параллелограмма равны: ∠ А=∠ С и ∠ В=∠ D.
Равенство первой пары идет из равенства треугольников АВD и CBD, а второй - АВС и ACD.
Теорема 24. Соседние углы параллелограмма, т.е. углы, прилежащие к одной стороне, составляют в сумме 180 градусов.
Это так, потому что они являются внутренними односторонними углами.
Теорема 25. Диагонали параллелограмма делят друг друга в точке их пересечения пополам.
Доказательство. Рассмотрим треугольники ВОС и АОD. По первому свойству AD=ВС ∠ ОАD=∠ ОСВ и ∠ ОDА=∠ ОВС как накрест лежащие при параллельных прямых AD и ВС. Поэтому треугольники ВОС и АОD равны по стороне и прилежащим к ней углам. Значит, ВО=ОD и АО=ОС, как соответственные стороны равных треугольников, ч.т.д.

Признаки параллелограмма
Теорема 26. Если противоположные стороны четырехугольника попарно равны, то он является параллелограммом.
Доказательство. Пусть у четырехугольника АВСD стороны AD и ВС, АВ и CD соответственно равны (рис2). Проведем диагональ АС. Треугольникик АВС и ACD равны по трем сторонам. Тогда углы ВАС и DСА равны и, следовательно, АВ параллельна CD. Параллельность сторон ВС и AD следует из равенства углов CAD и АСВ.
Теорема 27. Если противоположные углы четырехугольника попарно равны, то он является параллелограммом.
Пусть ∠ А=∠ С и ∠ В=∠ D. Т.к. ∠ А+∠ В+∠ С+∠ D=360 о, то ∠ А+∠ В=180 о и стороны AD и ВС параллельны (по признаку параллельности прямых). Также докажем и параллельность сторон АВ и CD и заключим, что АВСD является параллелограммом по определению.
Теорема 28. Если соседние углы четырехугольника, т.е. углы, прилежащие к одной стороне, составляют в сумме 180 градусов, то он является параллелограммом.
Если внутренние односторонные углы в сумме составляют 180 градусов, то прямые праллельны. Значит АВ парал CD и ВС парал AD. Четырехугольник оказывается параллелограммом по определению.
Теорема 29. Если диагонали четырехугольника взаимно делятся в точке пересечения пополам, то четырехугольник - параллелограмм.
Доказательство. Если АО=ОС, ВО=ОD, то треугольники АOD и ВОС равны, как имеющие равны углы (вертикальные) при вершине О, заключенные между парами равных сторон. Из равенства треугольников заключаем, что AD и ВС равны. Также равны стороны АВ и CD, и четырехугольник оказывается параллелограммом по признаку 1.
Теорема 30. Если четырехугольник имеет пару равных, параллельных между собой сторон, то он является параллелограммом.
Пусть в четырехугольнике АВСD стороны АВ и CD параллельны и равны. Проведем диагонали АС и ВD. Из параллельности этих прямых следует равенство накрест лежащих углов АВО=СDО и ВАО=ОСD. Треугольники АВО и CDО равны по стороне и прилежащим к ней углам. Поэтому АО=ОС, ВО=ОD, т.е. диагонали точкой пересечения делятся пополам и четырехугольник оказывается параллелограммом по признаку 4.

В геометрии рассматривают частные случаи параллелограмма.

Задача 1 . Один из углов параллелограмма равен 65°. Найти остальные углы параллелограмма.

∠C =∠A = 65° как противоположные углы параллелограмма.

∠А +∠В = 180° как углы, прилежащие к одной стороне параллелограмма.

∠В = 180° — ∠А = 180° — 65° = 115°.

∠D =∠B = 115° как противолежащие углы параллелограмма.

Ответ: ∠А =∠С = 65°; ∠В =∠D = 115°.

Задача 2. Сумма двух углов параллелограмма равна 220°. Найти углы параллелограмма.

Так как у параллелограмма имеется 2 равных острых угла и 2 равных тупых угла, то нам дана сумма двух тупых углов, т.е. ∠В +∠D = 220°. Тогда ∠В =∠D = 220°: 2 = 110°.

∠А +∠В = 180° как углы, прилежащие к одной стороне параллелограмма, поэтому ∠А = 180° — ∠В = 180° — 110° = 70°. Тогда ∠C =∠A = 70°.

Ответ: ∠А =∠С = 70°; ∠В =∠D = 110°.

Задача 3. Один из углов параллелограмма в 3 раза больше другого. Найти углы параллелограмма.

Пусть ∠А =х. Тогда ∠В = 3х. Зная, что сумма углов параллелограмма, прилежащих к одной его стороне равна 180°, составим уравнение.

х = 180 : 4;

Получаем: ∠А =х = 45°, а ∠В = 3х = 3 ∙ 45° = 135°.

Противолежащие углы параллелограмма равны, следовательно,

∠А =∠С = 45°; ∠В =∠D = 135°.

Ответ: ∠А =∠С = 45°; ∠В =∠D = 135°.

Задача 4. Докажите, что если у четырехугольника две стороны параллельны и равны, то этот четырехугольник – параллелограмм.

Доказательство.

Проведем диагональ BD и рассмотрим Δ ADB и Δ CBD.

AD = BC по условию. Сторона BD – общая. ∠1 = ∠2 как внутренние накрест лежащие при параллельных (по условию) прямых AD и BC и секущей BD. Следовательно, Δ ADB = Δ CBD по двум сторонам и углу между ними (1-й признак равенства треугольников). В равных треугольниках соответственные углы равны, значит, ∠3 =∠4. А эти углы являются внутренними накрест лежащими при прямых AB и CD и секущей BD. Отсюда следует параллельность прямых AB и CD. Таким образом, в данном четырехугольнике ABCD противолежащие стороны попарно параллельны, следовательно, по определению ABCD – параллелограмм, что и требовалось доказать.

Задача 5. Две стороны параллелограмма относятся как 2 : 5, а периметр равен 3,5 м. Найти стороны параллелограмма.

∙ (AB + AD).

Обозначим одну часть через х. тогда AB = 2x, AD = 5x метров. Зная, что периметр параллелограмма равен 3,5 м, составим уравнение:

2 ∙ (2x + 5x) = 3,5;

2 ∙ 7x = 3,5;

x = 3,5 : 14;

Одна часть составляет 0,25 м. Тогда AB = 2 ∙ 0,25 = 0,5 м; AD = 5 ∙ 0,25 = 1,25 м.

Проверка.

Периметр параллелограмма P ABCD = 2 ∙ (AB + AD) = 2 ∙ (0,25 + 1,25) = 2 ∙ 1,75 = 3,5 (м).

Так как противоположные стороны параллелограмма равны, то CD = AB = 0,25 м; BC = AD = 1,25 м.

Ответ: CD = AB = 0,25 м; BC = AD = 1,25 м.

Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!

Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.

Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.

Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.

Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля - до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.